十大排序
选择排序
这是最简单也最没用的算法, 时间复杂度有O(n^2), 同时也不稳定
选择排序的思路特别简单: 第一遍找到最小的值把它放在最前面, 再遍历一次找到第二小的数放到第二个位置......
那么我们怎么开始写这个程序呢?
首先第一步是要找到最小的那个数, 如果遍历到的arr[j]比最小位置还要小,那么就让minPosition = j, 所以
minPosition := 0
arr := []int{1, 3, 2, 4, 6, 5}
for j := 0; j < len(arr); j++ {
if arr[j] < arr[minPosition] {
minPosition = j
}
}
这样我们就可以在一次for循环中找到最小的那个索引, 但我们不止需要找到,我们还需要一次遍历所有的数找到并且做交换怎么办?
其实是需要这样做的.
for i := 0; i < len(arr); i++ {
minPosition = i
for j := i+1; j < len(arr); j++ {
if arr[j] < arr[minPos ition] {
minPosition = j
}
}
arr[minPosition], arr[i] = arr[i], arr[minPosition]
}
总结, 选择排序即, 选择一个最小的数并且把它放到正确的位置上,需要两个for循环.
冒泡排序
冒泡排序其实就是冒泡一样, 每次for循环有一个冒泡比较, 即相邻的元素的做比较, 如果arr[j] > arr[j-1] 则两个做交换, 这样一次下来至少有一个元素到达正确的位置上
那么第一次怎么让一个元素到它正确的位置上呢?
// 为什么是 j < len(arr)-1 呢
// 因为最后一个比较j+1会越界
for j := 0; j < len(arr)-1; i++ {
if arr[j] > arr[j+1] {
// 做交换
arr[j], arr[j+1] = arr[j+1], arr[j]
}
}
这样, 我们就可以把最大的一个数放到最后的一个位置上去
那我们不只是需要将一个数放到最大的位置上, 我们事实上是需要将所有的数都排一遍, 怎么做呢?
// 这里的i其实是比较的次数
for i := len(arr)-1; i > 0; i-- {
for j := 0; j < i; j++ {
if arr[j] > arr[j+1] {
arr[j], arr[j+1] = arr[j+1], arr[j]
}
}
}
插入排序
简单来说, 就像是打扑克牌, 就像打斗地主, 从小到大拿着, 这时候手里又有一张牌_____ 就是一个数组当前面有序的情况下, 当遇到新元素, 插入到前面位置上去
怎么插入到前面的位置去呢? 就是需要不断与前一个数做交换
for i := 1; i < len(arr); i++ {
// 与之前做比较
for j := i; j > 0; j-- {
// 不断与之前的数做比较
if arr[j] < arr[j-1] {
arr[j], arr[j-1] = arr[j-1], arr[j]
}
}
}
简单排序的总结
- 冒泡: 基本不用, 因为效率太低
- 选择: 基本不用, 不稳定
- 插入: 样本小, 而且有序的时候效率比较高
希尔排序---- 改进的插入排序
希尔排序 在排序的时候是需要一个间隔gap.
希尔排序可以看作是插入排序的加强版, 即有间隔gap距离去插入排序, 但由于是跳着排, 所以不稳定
那怎么写呢? 先把插入排序超过来, 因为希尔排序就是根据插入排序来的
for i := 1; i < len(arr); i++ {
// 与之前做比较
for j := i; j > 0; j-- {
// 不断与之前的数做比较
if arr[j] < arr[j-1] {
arr[j], arr[j-1] = arr[j-1], arr[j]
}
}
}
接着我们定义一个gap, 就是间隔的意思,
gap := 4
// i 应该是gap, i++ 的意思是 i应该不断++
for i := gap; i < len(arr); i++ {
// 与之前做比较
// 这里j变成j> gap-1了, 因为插入排序是连续比较到0, 而希尔则是比较gap-1次
for j := i; j > gap-1; j-=gap {
// 不断与之前的数做比较
if arr[j] < arr[j-gap] {
arr[j], arr[j-gap] = arr[j-gap], arr[j]
}
}
}
这样我们的希尔排序第一次就好了,按4比较一次, 那其实我们需要的不止是4, 我们需要可能是更多所以gap 也是不断减少的, 所以
for gap := 4; gap > 0; gap /= 2 {
for i := gap; i < len(arr); i++ {
// 与之前做比较
for j := i; j > gap-1; j -= gap {
// 不断与之前的数做比较
if arr[j] < arr[j-gap] {
arr[j], arr[j-gap] = arr[j-gap], arr[j]
}
}
}
}
归并排序
设计思想, 如果有两个有序数组,我们怎么对其进行排序? 思想是把它当作俩半截数组来排序
首先分配另外一个空间与原数组等长, 分配一个指针指向第一个位置, 再分配两个数组分别指向另外两个子数组的第一个位置, 接着就可以开始做比较了
通过比较两个半截数组的i和j 来不断放入到temp数组中
遍历结束, 通过放入两个半截数组剩下的元素, 结束temp数组
那么首先我们先这样做
arr := []int{........}
mid := len(arr)/2
// 新分配的数组空间
temp := make([]int, 0)
// i, j 分别指向第一个数组, 第二个数组的地一个位置
// k是temp的第一个位置
i, j, k := 0, mid+1, 0;
for i <= mid && j < len(arr) {
// <= 是稳定的
if arr[i] <= arr[j] {
temp[k] == arr[i]
i++
} else {
temp[k] == arr[j]
j++
}
k++
}
// 放入剩下的元素
for i <= mid {
temp[k] = arr[i]
k++
i++
}
for j < len(arr) {
temp[k] = arr[j]
j++
}
这样就是分开两个小数组的情况, 接下来我们就要开始递归了, 也就是不断分割数组的过程
我们首先改一下刚刚写过的函数, 应该更好用一点
这里其实就是处理merge的过程, 并且有了start, mid, end更好用了
func merge(arr []int, start, mid, end int) {
temp := make([]int, end-start+1)
i, j, k := start, mid+1, 0
for i <= mid && j <= end {
if arr[i] <= arr[j] {
temp[k] = arr[i]
i++
} else {
temp[k] = arr[j]
j++
}
k++
}
for ; i <= mid; i++ {
temp[k] = arr[i]
k++
}
for ; j <= end; j++ {
temp[k] = arr[j]
k++
}
// copy(arr[start:end+1], temp)
for m := 0; m < len(temp); m++ {
arr[start+m] = temp[m]
}
}
再接着需要一个mergesort的函数, 其实就是递归函数, 递归的结束条件是start == end
func mergeSort(arr []int, start, end int) {
if start == end {
return
}
mid := start + (end-start)/2
mergeSort(arr, start, mid)
mergeSort(arr, mid+1, end)
merge(arr, start, mid, end)
}
分了n次, 每层有比较交换的次数有logn次
总结, 归并排序的时间复杂度是O(n*logn), 其实还是快了不少的, 空间复杂度是O(n), 并且是稳定的
快速排序
如果我们要排序数组中从p到r的数据,我们选择任意一个数据为pivot, 并且遍历p到r1的数据, 将小于等于pivot的数据放到左边, 剩下的放到右边. 在接着递归就好了
i, j 指向的位置是i其实是比pivot小的区域, j是比pivot大的区域
func partition(arr []int, start, end int) int {
pivot := arr[end]
i := start
j := start
for ; j < end; j++ {
if arr[j] < pivot {
if arr[j] != arr[i] {
arr[i], arr[i] = arr[i], arr[j]
}
i++
}
}
arr[end], arr[i] = arr[i], arr[end]
return i
}
堆排序
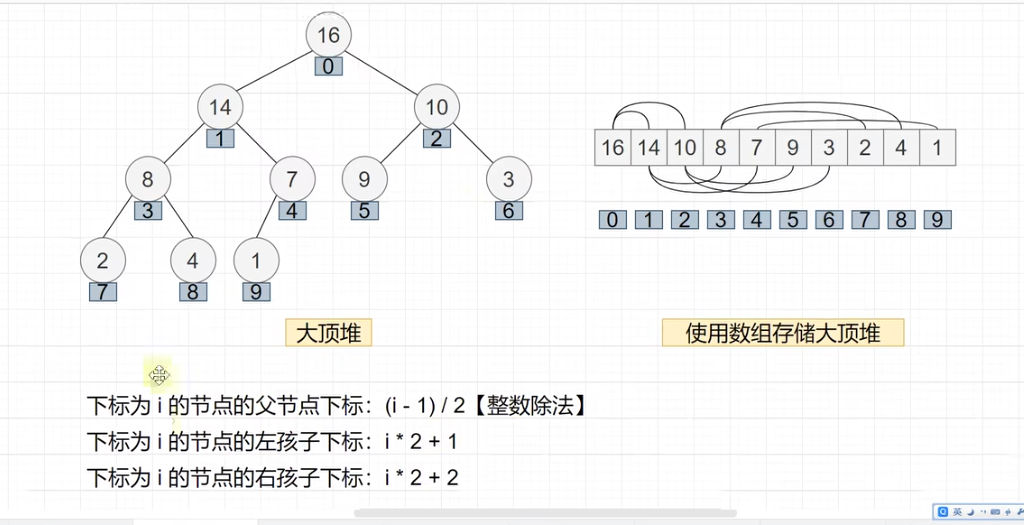
大顶堆就是父节点比两个子孩子都大, 使用数组来存储heap
下表为i的父节点下表是(i-1)/2 整数除法
下表为i的左子节点下表是i2 + 1
下表为i的右子节点下表是i2 + 2
维护堆的性质, 怎么维护呢?
如果有一个节点不符合大顶堆,即父元素比子元素小, 那么就把两个子孩子中大的那一个与父节点交换, 同时还要递归交换的子节点
heapify时间复杂度O(logn)
func heapify(arr []int, n, i int) {
largest := i
lson := i*2 + 1;
rson := i*2 + 2;
if lson < n && arr[largest] < arr[lson] {
largest = lson
}
if rson < n && arr[largest] < arr[rson] {
largest = rson
}
if largest != i {
arr[largest], arr[i] = arr[i], arr[largest]
heapify(arr, n, largest)
}
}
建堆
无序的数组怎么建堆呢?
以大顶堆为例, 建堆就是要维护父节点的值比两个子节点的值大--其实就是从最后一个节点的父节点, 不断往前开始堆化
for i := i/2-1; i >= 0; i-- {
heapify(arr, n, i)
}
即通过这样一个for循环就可以实现建堆的过程
建堆的时间复杂度是O(n)
怎么实现堆排序?
堆排序的过程就是,将最后一个子节点和堆顶的元素进行交换, 接着堆化堆顶的元素, 这样for循环结束就可以实现堆排序了
for i := n-1; i > 0; i-- {
arr[i], arr[0], arr[0], arr[i]
heapify(arr, n, 0)
}
这样就实现了堆排序, 堆排序对N个数进行heapify, 不稳定
总结:
- 时间复杂度(NlogN) 一个n的heapify的复杂度是logn, 总共有n个元素